2つないしはそれ以上の情報間の相互関係を“相関 correlation”といいます。
臨床検査データのまとめ方としてこの相関係数はよく利用されています。利用の仕方に間違いがないか考えてみる。単に相関係数と表現されるが幾種類かの相関係数が用意されています。その中でも代表的な2種類(通常よく用いられるピアソンの積率相関係数ともっと使われるべきスペアマンの順位相関係数)について書いてみます。
1.ピアソンの積率相関係数 Pearson’s product moment correlation coefficient
2組の測定値がどの程度よく一致しますかを-1~+1までの数値で表したものが相関係数で小文字のrを充てています。もしr=1であれば、両者の関係は完全に一致し、r=0のときは全く無関係で、r=-1では全く逆の関係にあることを示しています。
基本統計量にはxとyの共変動、x、yの偏差平方和が用いられます。
直線的な関係を知る尺度ですが、式の中には平均値が用いてあります。x変数、y変数ともに正規分布を前提に組み立てられています。nが充分大きいことが必要です。
下式が基本の式です。プログラムを組むためには下式が便利です。

1)ピアソンの積率相関係数を用いる場合の注意点には
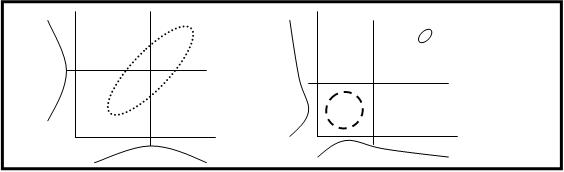
①図1のように、作図されたデータのほぼ中心に平均が位置づけされます。
この条件下でこそ相関係数は意味ある統計量を与えます。
図2のように左下にデータが集まり右上のはずれ値があるようなデータでは、見かけ上、相関係数が1日に近づきます。このように平均線を配置してみると分布とのズレが大きい場合、相関係数は間違った情報を与え「無意味」です。
②求められた相関係数の信頼性をいう場合には、相関係数に関する検定と推定が必要になります。rは1に近づけばより直線的な関係と見えますが、むしろr=0.6、0.4など相関があるのか無いのかといった場面でこそ検定と推定を行うことが必要です。
③相関係数は、式のとおり両端のデータにより大きく変動しますので検討した濃度範囲が問題になります。
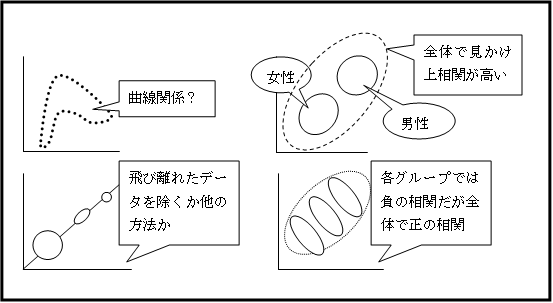
④相関係数はもともと直線的な関係を知るためのものです。従って曲線的な関係は考慮されません。
⑤相関係数が良くないのは属性の重なりのためではないか、分類したらどうなるのかということも、グラフと統計値を見て考える必要があります。
⑥相関係数が良すぎる場合に大きく飛び離れたデータの影響を受けていないか。平均値からのデータ数を比較してみることも必要になります。あまりにデータ数に差があると、分布を変換して正規化するか、他の相関係数を利用することも必要です。
⑦因果関係の有無を確認しておく。他の要因で見かけの相関を出していないか。

2)スペアマンの順位相関係数 Spearman’s rank correlation coefficient
rs :rに添え字のsをつける。
各変数ともに順位データに変換し相関係数を算出したもの。ピアソンの相関係数のように正規分布を前提条件にしないため利用範囲が大きい。
利点
①正規分布を問わない
②飛び離れたデータを除外せず、広範囲に利用できる
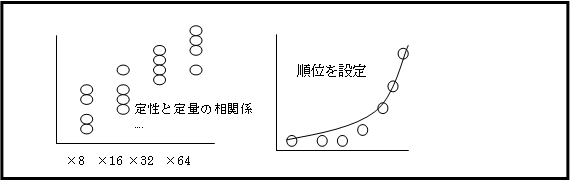
③定性・半定量の順序データも対象にできる
④直線的関係でない曲線関係などに適用できる
※同順位の処理:順位付け時に同じ順位が生じた場合に行う
同順位データの順位の平均値を各データの順位とします。
例 Xに8が2つあり3位,4位の順位が与えられた場合、両データの順位平均3.5位を両データに与え、この順位データをピアソン相関係数の計算と同じ方法で計算します。
<Excel関数:>
相関
CORREL 相関係数 =CORREL(配列1, 配列2)
PEARSON ピアソンの積率相関係数 =PEARSON(配列1, 配列2)
RSQ ピアソンの積率相関係数の2乗,寄与率 =RSQ(既知のy, 既知のx)
COVAR 2つのデータ間の共分散 =COVAR(配列1, 配列2)
順位
RANK 順位 =RANK(数値, 範囲, 順序)
RANK.AVG 同順位 =RANK.AVG(数値,参照,[順序])
参考資料・文献
1)竹内啓編:統計学辞典、東洋経済、1989
2)井野邦英:「臨床検査統計学講座Ⅱ」,全国社会保険技師会会誌、2000
3)井野邦英:データのまとめ方と考え方 第10版、2015
文責:井野邦英 アキュプレック